프로그래머스 정수 삼각형 java

전수민

Nov 13, 2025

TABLE OF CONTENTS

1. 문제에 대하여 📦

문제 링크: https://school.programmers.co.kr/learn/courses/30/lessons/43105

(1) 조건 분석 📊

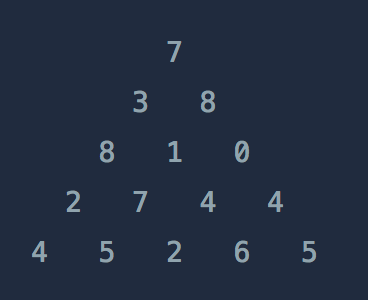
삼각형의 꼭대기부터 시작해서 밑으로 내려온다.

이때 내려올 때는 좌 대각, 우 대각으로만 내려올 수 있다. (예를 들어 맨 꼭대기 7에서는 3과 8로, 2열의 3에서는 8과 1로만 내려올 수 있다.)

이때 만나온 숫자들을 누적합할 때, 누적합의 최대값은?

2. 코드가 나오기까지 🛠️

KEY WORD: DP

각 좌표마다 이전 행에서 최고 좋은 경로를 선택했을 떄 숫자의 누적합을 표시할 예정이다. 꼭대기부터 밑변까지 차례대로 바텀업 해나간다. (출발지에서 시작함으로 바텀업) 도착지 입장에서는 이전 행 출발지 중 최대값을 찾고 그 값을 누적해 나가면 된다.

(1) 시간복잡도 분석 ⏳

이중 반복문 한 번 돈거랑 같다. 따라서 답은 다음과 같다.

$$
O(500 \times \frac{500 \times (500+1)}{2})
$$
삼각형 행의 최대값은 500임. 행이 500일 때, 열은 한 행마다 1부터 500까지 1씩 증가한다.

3. 코드 🌐

(1) SUDO CODE 💬


1. 꼭대기 바로 밑의 칸부터 다음을 반복
    (1)위의 행 좌우 값 중 큰값을 누적한다.
2. 밑변 중 최대값을 출력한다.

(2) JAVA CODE ☕


import java.util.*;

class Solution {
    static int R;
    public int solution(int[][] triangle) {
        R = triangle.length;
        for(int r = 1; r < R; r++){
            int col = triangle[r].length;
            for(int c = 0; c < col; c++){
                int left = (c-1 < 0? 0 : triangle[r-1][c-1]);
                int right = (c == col-1? 0 : triangle[r-1][c]);
                triangle[r][c] += Math.max(left, right);
            }
        }

        int max = 0;
        for(int c = 0; c < triangle[R-1].length; c++){
            max = Math.max(max, triangle[R-1][c]);
        }
        return max;
    }
}